1X Friction Profiles

[I wrote this content for Diamondback in 2017 when I was sponsored by them. As November 2020, you can still find it on the Diamondback blog, but you’re never sure whether these things will stick around. So unless I’ve posted something on Slowtwitch, where I have control over whether or not it sticks around, I thought it best to re-post it here for posterity. But I do encourage you to read this on Diamondback’s site (and maybe browse the bikes while you’re there!).]

Abstract

In this we cover:

• frictional losses due to lateral chain alignment
  • lateral offset – aka cross-chaining – does not have as large an effect as one might think
• frictional losses due to chain deflection – wrapping around the cogs and chainring (and, to a certain extent, the pulleys).
  • wrapping around cogs and chainrings is significant. To this end, running a 10T, for example, is less desirable than running a larger front ring – say a 54T or 56T – with a wider range cassette in the back. 56T-32 has less friction than 50T-28. While there are some obvious practical limitations here, 56-11/36 is actually a theoretically more “optimal” setup than 50-10/32. At least from the standpoint of friction.
• standard 2×11 drivetrains do not actually have 22 useful ratios. There are two issues: one is redundancy. The other is friction. Typically, a 2×11 has only about 14 distinct, usable ratios. That really changes the calculus when comparing to a 1×11 system.

So You’re Thinking About Flying Solo

The single front chainring of 1X drivetrain would seem to be a huge compromise. Aren’t you giving up half of your gears? To understand what you’re actually sacrificing, we need to look at how usable all the gears in a standard 2X system are, as well as how many distinct ratios exist. A standard 53-39 2×11 drivetrain actually has only about 18 distinct gear ratios; imaging a typical 53-39 paired with an 11-26 cassette, we see that, for example, 53-15 is virtually identical to 39-11. And there are several such other overlapping ratios in most standard configurations; the exact number will vary depending on the cassette and chainring combinations, but typically there are 3-4 redundant ratios. For 53/39-11/26, they are: 53-15 & 39-11, 53-19 & 39-14, 53-23 & 39-17, and 53-26 & 39-19.

It’s worth noting that assuming only a 5rpm range in preferred cadence does a lot to further tighten up the relative number of distinct ratios. For example, 53-23 at 85rpm travels the same effective gear-inches per minute as 39-16 at 80rpm. Most cyclists have a preferred cadence. But there’s some obvious variance built in. And ±2rpm seems typical. If you realize that you aren’t wedded to a single fixed cadence, the relative number of redundant ratios goes up.

Beyond redundancy, however, is the issue of usefulness. For the purposes of this article, we will define usefulness solely based upon losses to friction. Chain-based drivetrains experience losses for two reasons:

• losses due to lateral deflection of the chain. The more a chain is deflected laterally, the larger the losses. As the chain deflects laterally, the plates rubs against each other, causing frictional losses. This is what is called “cross-chaining,” and this is easily to visualize.
• losses due to chain articulation. These come as a result of the chain bending around a cog or a chainring. The most critical detail here is that the more a chain deflects, the larger the losses. Wrapping around an 11-tooth cog results in significantly higher losses than wrapping around a 28-tooth cog because the chain has to bend more, and the more it bends, the more it experiences losses to friction. This is significantly less intuitive than losses due to chain deflection, but the magnitude of potential losses here is quite high, higher even in the worst case scenarios than even the most extreme cases of lateral deflection.

As a result of these two factors working either in concert or in opposition, cross-chaining is not equally bad. Cross-chaining small-chainring to small-cog incurs enormous frictional losses. But cross-chaining large-chainring to large-cog incurs much less. It is this fact that really proves to be the saving grace of 1X systems.

The data referenced herein was produced by Jason Smith, founder of friction-facts.com and current Chief Technology Officer for CeramicSpeed. To isolate the differences in frictional losses between lateral chain alignment and chain articulation, Jason first did frictional testing with perfectly aligned chainring-cog pairs and then subtracted from total frictional losses in a complete drivetrain (recreated on his lab bench) to come up with losses due to lateral alignment.

Near the end of 2016, CeramicSpeed, which had previously acquired the UFO (Ultra-Fast Optimization) chain business from Jason Smith, purchased the rest of the business and brought him on board as their new CTO. The testing referenced here predates this acquisition. This article also contains references to other testing done by Jason on 1X systems, in particular Jason’s own testing of XSync (AKA “narrow-wide”) chainrings developed by SRAM for chain-retention. For those not familiar, this is why front chainrings for 1X only come in even numbered sizes – 48T, 50T, 52T, etc. The teeth on the chainring alternate “narrow”-teeth (really what is standard on a typical chainring) and wide-teeth, which more fully engage the wider spaced links of chain. Jason found (perhaps unsurprisingly since it is a purely static interface) that narrow-wide chainrings do not add any measurable frictional losses to the drivetrain.

In the course of reviewing my work here for accuracy, he elaborated on why this is so,

I speculate the reason Narrow Wide rings do not create additional friction, in cross chaining situations (pure aligned situation makes sense that the NW don’t increase friction b/c the chain is not ‘rubbing’ on the teeth; the chain drops perfectly on the teeth with no or minimal side rubbing), is as follows- with a standard ring, the link side plates rub on every other tooth. With, say, X amount of lateral force. With NWs, the chain side plates rub on every tooth, but with with X/2 amount of force. This is because with NWs, each & every tooth is ‘pulling’ the laterally deflected chain into alignment, but the lateral distance the chain is being pulled is half that of std rings, but twice as often. We have a case of 1/2 times X or 1 times X/2. The same.

The Effect of the Clutch Rear Derailleur

There are two other potential considerations when considering the friction profile of 1X vs 2X drivetrains that we will not cover here since data are not yet available. The primary consideration is the additional tension in the lower span of the chain due to the stiffer spring in what are called “clutch” rear-derailleurs. Because dropping a chain is such a catastrophic occurrence with a 1X system, chain retention is a huge priority.

Dedicated 1X derailleurs have a couple unique features. Firstly, they are straight, not slant, parallelogram designs, which means they sweep a different arc (travel is limited exclusively to the horizontal axis) when they move, which helps to prevent ghost-shifts due to the inevitable inward-movement that accompanies downward-movement on a slant parallelogram design. (As an aside, this does  make extremely precise B-limit screw adjustments an absolute necessity for proper shifting on a straight-parallelogram derailleur.)

They also have what SRAM calls a “Roller Bearing Clutch” to prevent chain slap (not really an issue on road bikes) and bounce and to help with retention during shifts. Mountain bikes have used clutch RDs even on 2x setups because it prevents chain bounce; the clutch in this case is a one-way bearing, which permits movement in one direction, but not in the other. It’s not exclusively one way – it’s a friction-based design – because otherwise the derailleur couldn’t function (since the lower knuckle needs to be able to move somewhat freely as you shift to take up and let out chain slack). Because of this, the derailleur requires a much stiffer and stronger spring to return the derailleur to higher gears as you let tension off the shifter cable.

It’s clear that this spring must increase tension in the lower span, which should thereby increase frictional losses in the system. What’s not clear, however, is how much. But we can make some educated estimates.

Most of the research of chain tension covers gross efficiency, which typically goes up as power goes up. This is because there is a fixed amount of loss from chain articulation and lateral alignment that becomes a smaller and smaller percentage of the total power provided by the system. In other words, simply moving chain over the pulleys, cog, and chainring incurs losses. But as chain tension goes up from pedaling harder, those losses do not increase proportionally, because there is absolutely no tension between the links engaged by the cogs. However, the losses do increase. At least, in most studies. In David Gordon Wilson’s classic, Bicycle Science, he shows that a rider putting out 400w has a gross efficiency of about 98% (8w of losses). At 50w, it’s about 94% (3w of losses). But that didn’t account for variance in cadence, which can have a significant effect on frictional losses.

In “Human Power,” the HPV journal, James Spicer did a 2000 study where he was able to isolate these variables. In 52-15 and 60rpm and at 100w, Spicer measured efficiency at 92.3%. At 175w and the same gearing and cadence, he measured efficiency at 97.5%. Converting from percentages to straight wattage losses, that means at 100w, frictional losses cost 7.7w. At 175w, frictional losses cost only 4.375w, so lower both in relative and absolute terms. Spicer himself struggles a bit to make sense of this.

Clearly, these data indicate that the fundamental operation of the drive must be related to the chain tension such that the efficiency increases with increasing tension even though the frictional losses should increase

Spicer further found – albeit in limited testing – that frictional losses due to lubrication were, “minimal” and did not vary significantly among the lubricants he tested. This is not supported by Jason Smith’s own testing. So I asked Jason what he made of this. He had an answer already made, courtesy of a similar inquiry made by Lennard Zinn in 2013.

As I’ve mentioned before, Spicer et al’s paper has many correct conclusions. However, with regard to tension versus efficiency, they made a major incorrect assumption in the paper by not segregating the frictional contribution of the chain as it snakes through the pulleys. From Spicer et al’s paper, “Since the chain tension is large only on one side of the drive, this loss only has significant contributions at two points — at engagement of the chain on the front chain ring and departure on the rear sprocket.”

They did not consider the effects of the lower spans’ friction in their formulas and calculations, and assumed all friction was due to the top span. We now know that approximately two-to-three watts of friction is created by the lower pulleys and the lower three chain spans due to the applied two-ish pounds of tension from the derailleur arm. We know that it does not vary due to rider load or corresponding chain tension. Spicer et al assumed the total friction he was measuring was due to only the top span, when actually, it is a joint contribution from the top span and the fixed-friction lower spans.

Because the lower span friction does not vary with upper span tension, their incorrect assumption skewed the linearity of the friction versus top tension and efficiency versus top tension graphs, and therefore their overall results with regard to efficiency versus tension. Additionally, when they plot out their tension versus efficiency results, the efficiency exceeds 100 percent in all three sprocket test cases at higher rider output. This, if correct, would be the discovery of perpetual motion. According to their data, any Tour rider with high enough power output would actually be propelled by the drivetrain rather than slowed by it.

The FF test “Chain Efficiency vs. Load” has two graphs [shown above and below]. The first is the total drivetrain losses vs. friction. Note the zero offset. It is a standard Y=MX+B equation. This fixed offset is due to the pulley and lower span friction, and the linear increase in friction with load is due to the top span. The second graph plots this as an efficiency percent versus load. Now, the efficiency versus load graph is non-linear, and correctly shows a trend of increasing efficiency with increasing load. However, this non-linear increase is not due solely to the friction of the top span. It is due to the combination of the fixed friction in the lower pulley spans and linear increasing top span.

Based on Jason’s research, you clearly cannot ignore tension in the lower span. So how much tension does the clutch RD add? Since it’s a spring, it does depend on the position of the derailleur cage. But we can look at what is typical. Jason estimated that the clutch derailleurs apply a force of about 4.5lbs. For comparison, a standard Shimano Dura-Ace RD applies about 3.2lbs of force to the lower span in typical positions with a properly sized chain. I decided to test this using a relatively simple technique – I used my small – and very precise – Acaia coffee scale to move the derailleur cage. The number jumped around a bit, but I was able to pretty closely see that it was almost exactly a force of 2000gf. 2000gf = 2kgf = 4.4lbf. Unsurprisingly, Jason’s estimate was pretty much spot on.

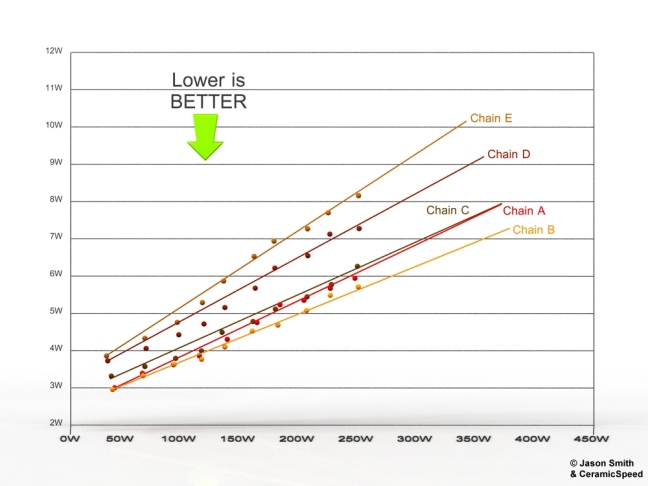
Jason had used his 4.5lb estimate for spring force to then further estimate additional losses in the lower span,

To make a guesstimate, I reviewed the FF reports on OSPW systems, which compare lighter derailleur tensions to a standard RD tesnion. The linear relationship can be applied to an RD with higher-than-standard tension. The standard Shimano RD creates an average of 3.19lbs of chain tension on the lower three spans. Here’s my guess- let’s say a clutch RD system creates 4.5 lbs of chain tension. Because the friction created by the lower three spans is pretty close to linear with the chain tension created by the spring (all other factors equal), then the clutch would create about 40% more friction than a standard RD. This would go from, say, 3-ish watts (referencing the y-intercept) to about 4-ish watts. Without doing the test, I’m going to say about a watt or slightly more increase occurs with a clutch RD.

The Effect of Pulley Wheels

The second issue relates to pulley wheels. The stock pulleys on SRAM’s Force1 RD spin on mid-tier cartridge bearing. They are comparable to other Force-level RDs, but we know that the frictional losses of these bearings as compared with the higher quality bearings found in their RED rear derailleurs are measurably different. But I don’t believe they are significant. In previous testing, between the very best pulleys – which incur practically zero frictional losses – and the very worst, it was merely 1.309w per pair. And that was for super high end versus Shimano Acera. Standard Force/Rival level pulleys – similar to what is found on Force1 – had frictional losses that were less than 0.3w per pair.

CeramicSpeed does make 1X-specific (narrow-wide) pulley wheels that eliminate this issue, but it represents a significant price upgrade. Stock RED pulley wheels with ceramic bearings are about 3x the price per pair (about $100/pair versus about $30/pair for Force1). But CeramicSpeed pulley wheels are about 12x the price, starting at $379/pair. Unfortuntely, there isn’t much in the middle. It would be nice to see SRAM offer a RED-level equivalent option for pulley wheels here, but it shouldn’t be a big factor in terms of drivetrain losses.

One bit of good news for 1X is that, because the pulley wheels are narrow-wide, they have to have an even number of teeth. Force1 pulleys are 12T, instead of the standard 11T found on SRAM’s other rear derailleurs, meaning they spin just under 8% slower. This can help to offset the frictional losses of the lower quality bearings, and, given how small the losses are here anyway, this might be enough to eliminate the discrepancy entirely. Based on Jason’s own testing of pulley wheels, the jump from 11T to 12T alone accounts for about 0.1w per pulley wheel (dependent on chain speed, of course). Meaning, in total, the clutch rear derailleur should add about 0.8w to the total system (1.0w – 2×0.1w).

Frictional Losses in The Chain

With that out of the way, let’s look at the losses due to lateral chain alignment and to chain deflection from wrapping around cogs/chainrings. Jason Smith used the following test set up was used to measure these losses:

The test was performed with an 11sp Shimano CS-9000 11-28T cassette, Shimano FC-9000 53T big ring, and FC-9000 39T small ring, 95RPM cadence, and 250W rider output. Two 11sp chains were used for all test points; a Shimano Dura-Ace 11sp CN9000 and a SRAM 11sp PC Red 22. The data points in the following graphs represent the average of both chains’ measurements.

Lateral Alignment (“Cross Chaining”) Losses

What impact does lateral deflection have? It has some, but it’s not nearly as much of an issue as you might think. Now, some of this may be due to more precise chain manufacturing techniques. Eleven – and now twelve – speed chains are remarkable pieces of precision engineering. They are strong, reliable, and supremely flexible. All in a package that just keeps getting narrower and narrower. I believe that the increased precision required to make 11 and 12 speed chains plays a big role in minimizing the losses due to cross chaining. Would we see these same results with a beefy 6 speed chain? It’s not clear, though I think it is unlikely. Of course, the maximum amount of cross chaining that can be achieved with a 6-speed cassette is also significantly lower due to narrower hub spacing. Regardless, with the chains we do have, you can cross-chain quite a lot without incurring a significant frictional penalty.

To understand the range of potential losses, first, we need to stipulate the ratios where perfect alignment occurs. Assuming relatively standard BB spacing, the large chainring is perfectly aligned with the 4th cog (53-14 with out hypothetical 11-28) and the small chainring is perfectly aligned with the 6th cog (39-17). What this means is that the maximum amount of cross-chaining that can occur is seven cogs. Typically, 1X rings are offset towards the middle (meaning aligned with the 5th cog), meaning the maximal misalignment for 1×11 setups is six cogs instead of seven.

Looking at 48T-10/34, we see,

Gear range is 1.33:4.80, compared to 1.39:4.82 with the 39-53 11-28 2×11.

Very similar overall gear range compared to the 2×11.

Frictional losses at lower gearing are similar or slightly less on average compared to the 2×11.

Frictional losses at higher gearing are greater than the 2×11, by approximately 1.0 watts.

Looking at 56-12/34, Jason found,

Gear range is 1.65:4.66, compared to 1.39:4.82 with the 39-53 11-28 2×11.

Slightly narrower overall gearing range on both high gearing and low gearing sides.

Frictional losses at lower gearing are less on all of the lower gears by more than a half watt on average, compared to the 2×11.

Frictional losses at higher gearing are very similar to the 2×11.

Based on the above data, our 52-11/32 or 54-11/36 setups are not going to have measurably more friction than a comparable 2×11 setup. And, given that we know that a 2×11 is really more like 14 gears rather than 22, it doesn’t give up all that much in the way of ratios either. If you want to run 1X, the facts about friction certainly shouldn’t dissuade you.

Conclusions

Ultimately, the frictional losses provide two distinct and somewhat surprising conclusions. The first is that, from a frictional standpoint, typical 1X setups pay no significant penalty vs comparable 2x setups. The second, and perhaps more surprising thing, is that you want to run as large a front chainring and as wide a range cassette as possible.

While the intent of this article was to do a hard analysis of the comparative frictional losses between drivetrains, it leaves out two important points. The first is that a shifting is simpler with a 1X. You never have to shift the front. In my own experience, this is extremely valuable, though obviously subjective. It’s clear that remembering when to shift big-to-small and small-to-big can have a real impact on frictional losses in your drivetrain. And remembering when to do that at mile 100 of an Ironman is a lot harder than it is while you are out for an easy spin. (This also doesn’t consider the frictional losses due to making those shifts, which are likely not significant given how often one tends to shift the front, but which are still worth considering.) But really, it’s the mental benefit here that’s big. It’s just one less thing to think about.

But what about aerodynamics? 1X systems lack a front derailleur. The drag cost of a front derailleur, based on reports of testing, varies quite a bit based on frame design. But it can be “significant” (order of magnitude of approximately 5.0w). While I initially approached Jason for his research on the frictional losses in 1X drivetrains, he actually was privy to wind tunnel data on 1X systems as part of his compilation of this data. The data that he saw, between -5 and +5 degrees of yaw, showed a gain of 3w for removal of the FD and mount versus a system with a front derailleur. This fits with data I have seen – hence my reference of “order of magnitude of 5w,” with the acknowledgement that there can be significant variance based on the frame being tested. Also, unfortunately, in all cases – unlike with the frictional data – this is data that is not available for public consumption, precisely because it does vary so much based on the frame.

Given that the frictional losses do not provide a compelling reason not to run 1X, the aerodynamic argument can then become primary. There is significant variance here based on frame design and how easy (or not) a given frame is to convert to 1X – for example, is the derailleur hanger easily removable. Nevertheless, in the best cases, it represents a meaningful aerodynamic savings that, when coupled with the knowledge that frictional losses are not a concern, provides an overall advantage on course.